- Community
-
Programs
- Schools
-
Careers
- RN Specialties
- Best RN Jobs and Salaries
- Aesthetic Nurse
- Nursing Informatics
- Nurse Case Manager
- NICU Nurse
- Forensic Nurse
- Labor and Delivery Nurse
- Psychiatric Nurse
- Pediatric Nurse
- Travel Nurse
- Telemetry Nurse
- Dermatology Nurse
- Nurse Practitioner
- Best NP Jobs and Salaries
- Family NP (FNP)
- Pediatric NP
- Neonatal NP
- Oncology NP
- Acute Care NP
- Aesthetic NP
- Women's Health NP
- Adult-Gerontology NP
- Orthopedic NP
- Emergency NP
- Psychiatric-Mental Health NP (PMHNP)
- APRN
- Nurse Educator
- Nurse Administrator
- Certified Nurse Midwife (CNM)
- Clinical Nurse Specialist (CNS)
- Certified Registered Nurse Anesthetist (CRNA)
- Resources
- Education
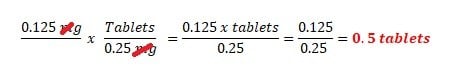
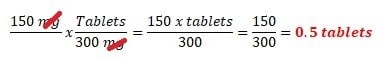

btf4
49 Posts
(question)1. An oral tablet has strength of 0.25 mg. The order is to give 0.125 mg. How many tablets will the nurse give?
Do I do it like this? "X" tablet= 0.25 mg * 1tab/0.125 = 2 tabs?
Or like this? "X" tablet =0.125 mg * 1tab/0.25mg= 0.5 tabs?
(question)2. A client is ordered 150mg of aspirin. 300 mg aspirin tablets are available. How many tablets would you give?
This question has similarities with question number 1, but where I get confused is where do I put my "X" under the strength? Or the order?